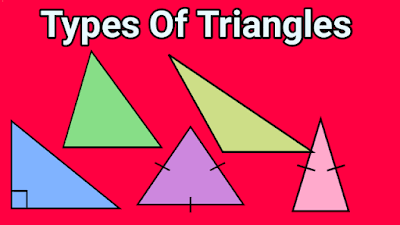
In our daily life, we have to deal with different kinds of shapes. In these shapes, some shapes are opened and some shapes are closed. To differentiate these shapes, we have kept the names of these shapes. Therefore, a closed figure which has three sides that are connected is known as a triangle. Along with three sides, a triangle has also three angles. Based on these sides and angles, triangles are classified into different types. Here, we will discuss all types of triangles with the help of pictures.

Triangles Classified by Sides

Based on sides, triangles are classified into three categories. These three categories of the triangles based on sides are explained below;

1. Scalene Triangle

A scalene triangle is such a triangle which has different lengths of its sides. It means that there are not congruent sides in the scalene triangle. Along with different lengths of sides, the measures of all the angles of this triangle are also different.

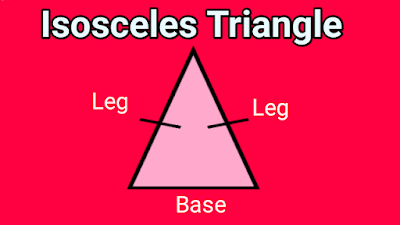
2. Isosceles Triangle

A triangle which has two congruent sides (same lengths) is known as an isosceles triangle. The two sides of the isosceles triangle which have same lengths are known as legs and the third side of this triangle which has a different length is known as base. The angle which is formed by two congruent sides of an isosceles triangle is known as vertex angle and the other two angles are known as base angles. The most important quality of this triangle is that the base angles of this triangle are of equal measurement.

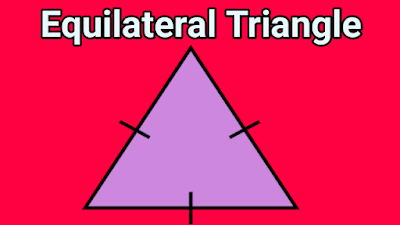
3. Equilateral Triangle

It is an essential kind of triangle concerning sides because this triangle has three sides of equal lengths. In other words, we can say that an equilateral triangle is a triangle which has all the three sides congruent. We can also say an equilateral triangle as a regular triangle because along with three equal sides, this triangle has also three angles of equal measurement. As the total measurement of all the angles of a triangle is 180°. Therefore, each angle of an equilateral triangle is 60°.

Relevant Posts:

Difference Between Rational and Irrational Numbers

Types of Sets In Mathematics

Triangles Classified by Angles

Based on the angles, we can classify these triangles into five different categories. These five categories of the triangles based on angles are explained below;

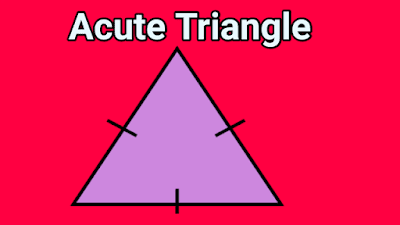
4. Acute Triangle

As we know that there are three angles of a triangle. If all the angles of a triangle have less than 90°, this triangle is known as an acute triangle. The most important quality of this triangle is that it can be an isosceles, scalene or equilateral triangle.

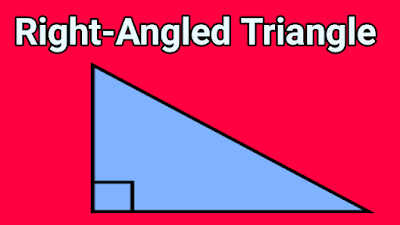
5. Right-Angled Triangle

A triangle which has at least one right angle (an angle of exact 90° measurements) is known as a right-angled triangle. A right-angled triangle can be an isosceles or scalene triangle but it can’t be an equilateral triangle.

6. Obtuse Triangle

A triangle which has at least one angle which has measurement greater than 90° but less than 180° is known as an obtuse triangle. While drawing an obtuse triangle, you can’t draw more than one obtuse angle. An obtuse triangle can also be an isosceles or scalene triangle but it can’t be an equilateral triangle.

7. Equiangular Triangle

A triangle which has all three angles of equal measurement is known as an equiangular triangle. It means that all the angles of a triangle should be 60°. All the equiangular triangles are also equilateral.

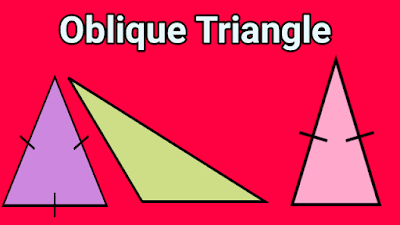
8. Oblique Triangle

A triangle which is not a right-angled triangle is known as an oblique triangle. It means that an oblique triangle can be either an acute triangle, obtuse triangle, equiangular triangle but it can’t be a right-angled triangle.

Basic Properties of Triangles

Along with understanding different types of triangles, it is also necessary for us to get an idea about the basic properties of the triangles. These properties are explained below;

· According to the angle sum property of a triangle, the sum of all the angles of a triangle should be 180°.

· If we add two sides of a triangle, their sum will be greater than the third side of the triangle.

· The side which is opposite to the largest angle of the triangle is known as the largest side of the triangle.

· If we know two sides of a triangle, we can easily find the third side of the triangle by using Pythagorean Theorem.

· If we know the two angles of a triangle, we can easily find the third angle of the triangle by using the angle sum formula of a triangle.

Real-Life Example of Triangles

It is a fact that if we want to teach the basic concept of triangles to the students, we will have to give real-life examples of triangles to the students. Some essential and interesting real-life examples of the triangles are given below;

· Most of us see traffic signs daily. These traffic signs are the best examples of the equilateral triangles because all the angles and sides of these traffic signs are equal.

· Bermuda triangle is also known as another real-life example of the triangles. Bermuda triangle is a loosely defined triangular area in the Atlantic Ocean. In the Bermuda Triangle, more than 50 ships and 20 aircraft are my sterically disappeared.

· Pyramids are also the best real-life examples of the triangles. These are ancient mountains that were constructed by the Egyptians. The shapes of these pyramids are tetrahedral i.e there are four triangular regions in these ancient mountains.

· To support the bridges, triangular shapes are constructed. These triangular shapes are known as Truss bridges. These supporting shapes can distribute the weight of the bridges.

· Sailing boats are also the best real-life examples of triangular shapes. Some years ago, the designs of these shapes were square but nowadays, almost all the sailing shapes have triangular designs.

· The roofs of the houses are triangular. These shapes of the roofs don’t allow rain and snow to stay for a longer period.

· While constructing the staircases, the constructors use knowledge of triangle. Its reason is that they have to build these staircases in the triangular form. These staircases form the right-angled triangles. When we have to place the staircase in front of a wall, we have to make a triangular shape.

· To make some buildings appealing and interesting, these buildings are constructed in the triangular shape. The most important example of these kinds of buildings is the Eiffel Tower.

· We have to use triangular formulas to find the height of a pole or a mountain. For this reason, we use the concept of a right-angled triangle.

· Sandwiches and pizzas are the most favourite foods for the young generation. Most of the people start their day by eating sandwiches and the shape of these sandwiches is also triangular. Some pizzas are also available in the triangular shape.

BZU SCIENCE

Types of Triangles with Pictures